Novel machine learning approaches are revolutionizing scientific research, but they did not emerge out of the blue. Decades of methodological developments and applications in scientific computing have culminated in a paradigmatic shift in the way science will be conducted in the twenty first century. I am interested in modernizing classical scientific computing approaches, such as numerical integration, numerical continuation, and bifurcation analyses, utilizing modern GPU hardware to accelerate analysis of complex dynamical states, including limit cycles, invariant tori, and chaotic attractors. As an active developer for the open source PySINDy package, I am also investigating applications and methodological developments of machine learning system identification algorithms. I am also interested in automated coordinate and symmetry discovery via neural network autoencoders and the dynamic mode decomposition. I aim to demonstrate this approach on complex systems to advance discovery in pattern formation.
Related works
[2] Nicolaou and Motter, From a Point to a Torus: Unveiling Emergent Dynamics with Higher-order Bifurcations SIAM News 57, 1 (2024).
[3] Nicolaou and Bramburger, Complex localization mechanisms in networks of coupled oscillators: two case studies, Chaos 34, 013131 (2024).
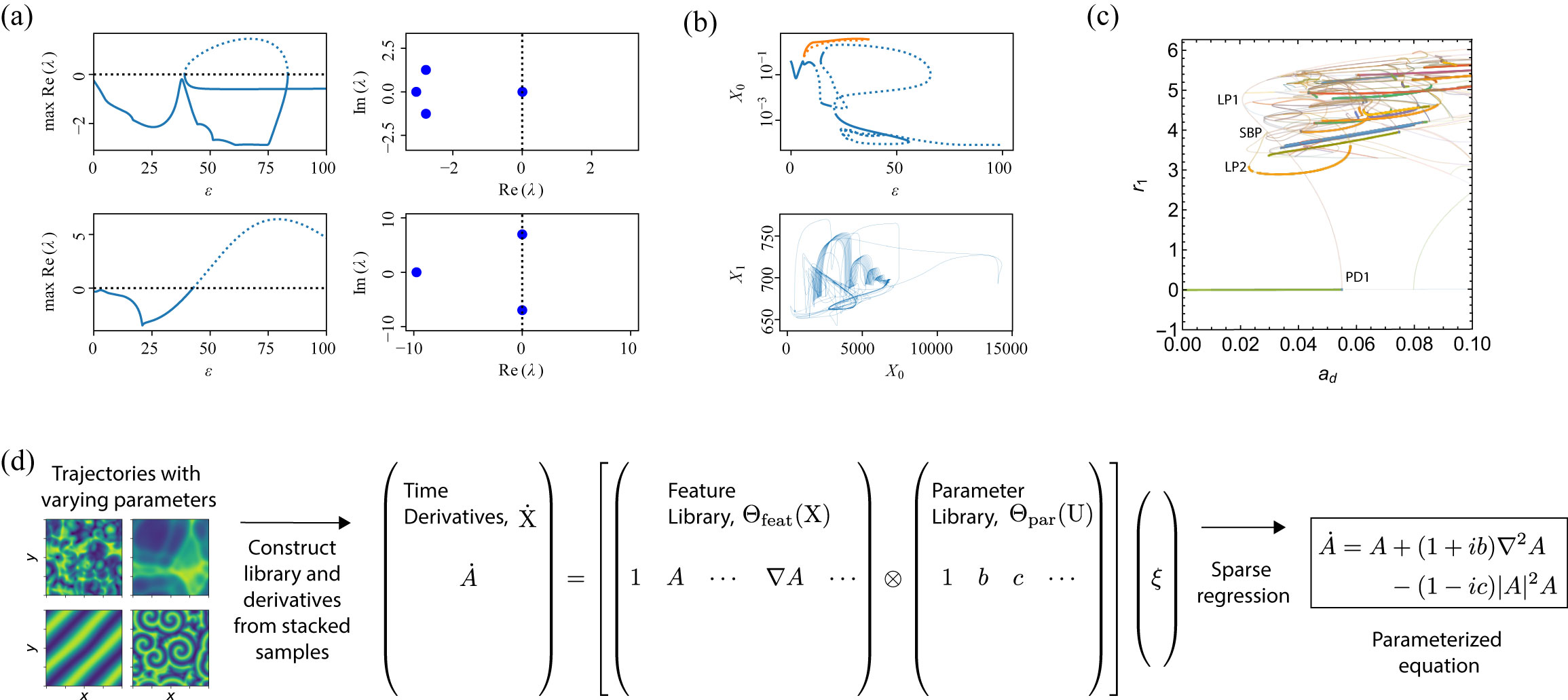
[5] Nicolaou, Guo, Chen, Brunton, and Kutz, Data-driven discovery and extrapolation of parameterized pattern-forming dynamics, Phys. Rev. Research 5, L042017 (2023).
[6] Nicolaou, Nicholson, Motter, and Green, Prevalence of multistability and nonstationarity in driven chemical networks, The Journal of Chemical Physics 158, 225101 (2023).
[7] Kaptanoglu, Zhang, Nicolaou, Fasel, and Brunton, Benchmarking sparse system identification with low-dimensional chaos Nonlinear Dynamics 111, 13143–13164 (2023).
[8] Kaptanoglu, de Silva, Fasel, Kaheman, Goldschmidt, Callaham, Delahunt, Nicolaou, Champion, Loiseau, Kutz, and Brunton, PySINDy: A comprehensive Python package for robust sparse system identification, J. Open Source Softw. 7, 3994 (2022).